English version
Versione italiana
A snake moving through the grass and the sheath of a parasitoid wasp buckled during the insertion of the ovipositor are a couple of examples among many others in which nature inspires the research on extreme structures. These are elastic structures, the same on which students of civil or mechanical engineering struggle learning structural design, but now considered undergoing large displacement and thus working in a fully nonlinear regime. Unlike bridges or airplane wings, which are subject to small deflections, the displacements of a snake or of a wasp sheath are so large that nonlinear effects, usually neglected in engineering design, are the key to reach extreme functionalities.
The 'Instabilities' ERC advanced grant led by prof Davide Bigoni is devoted to the study and development in the field of nonlinear Solid and Structural Mechanics.
Combining the study of elastic rods subject to large deflections (in other words the study of the ‘elastica’) with the analysis of snake motion has led the research team to invent the so-called ‘elastica arm scale’, a new type of balance with deformable arms, in which a fusion of the concepts of equilibrium and deformation has been achieved (Fig. 1). Snake locomotion has also inspired the idea of torsional locomotion, which can be easily explained through the proof-of-concept device realized by the research team and nicknamed 'torsional gun', where a longitudinal propulsion is generated through a torsional action (Fig. 2). Finally, the equations of the elastica are also the same governing the shape of a liquid droplet, an analogy that has been exploited by the research group to demonstrate, for the first time, the ‘dripping of an elastic rod’ (Fig. 3). For details:
http://erc-instabilities.unitn.it/disseminationtraining.php
The Instabilities research group is also active in analyzing nonlinear deformation of solids, to explain for instance folding of the earth crust, to design of new ultraresistant materials or metamaterials making objects invisible to vibrations.
But that is another story. A story that can that can be heard after knocking the door of Bigoni's office at DICAM.
IL MONDO MAGICO DELLE STRUTTURE ESTREME
La bilancia a bracci elastici, l’arma torsionale e il dripping di un’asta elastica
Un serpente che si muove nell'erba o il pungiglione inflesso di una vespa parassitoide intenta a iniettare le proprie uova sono solo un paio di esempi in cui la natura suggerisce il concetto di struttura estrema, ovvero una struttura elastica, proprio come una di quelle su cui impazziscono gli studenti di Scienza delle costruzioni, ma ora soggetta a grandi deformazioni e quindi in un regime di lavoro non-lineare. A differenza dei ponti e delle ali degli aerei, che sono soggetti solo a flessioni piccolissime, gli spostamenti di un serpente o del pungiglione sono così grandi che gli effetti non-lineari, spesso trascurati nella progettazione degli ingegneri civili o meccanici, diventano la chiave per raggiungere funzionalità estreme.
Il progetto di ricerca ERC advanced grant ‘Instabilities’, coordinato dal prof Davide Bigoni è dedicato allo studio e allo sviluppo nel campo della meccanica dei solidi e delle strutture e coinvolge un team internazionale di ricercatori con base al Dipartimento di Ingegneria Civile, Ambientale e Meccanica (DICAM).
Combinando lo studio delle aste elastiche in regime non-lineare (lo studio dell'elastica di Eulero) con l'analisi della locomozione dei serpenti, il team di ricercatori ERC ha inventato la ‘bilancia a bracci elastici’, uno strumento in cui si realizza la fusione dei concetti di equilibrio e deformazione su cui sono basate le bilance classiche (Fig. 1). I meccanismi di locomozione dei serpenti hanno anche ispirato l’idea della ‘locomozione torsionale’, che può essere semplicemente introdotta attraverso lo strumento proof-of-concept sviluppato dal gruppo di ricerca ERC e chiamato scherzosamente ‘arma torsionale’, con cui viene ottenuta una propulsione longitudinale da una azione torsionale (Fig. 2). Infine, poiché le equazioni dell'elastica di Eulero sono le stesse che governano la forma di una goccia di acqua, il gruppo di ricerca ERC ha pensato di potere sfruttare l'analogia per dimostrare un fenomeno simile alla formazione di una goccia, ma che coinvolge una asta elastica, ovvero il dripping (Fig. 3). Per dettagli, consultare:
http://erc-instabilities.unitn.it/disseminationtraining.php
Il gruppo di ricerca ERC Instabilities è anche attivo nello studio delle deformazioni nonlineari dei solidi, per spiegare, per esempio, le pieghe della crosta terrestre, ma anche per progettare nuovi materiali ultraresistenti o metamateriali per rendere invisibili oggetti alle vibrazioni. Ma questa è una altra storia... che si può sentire raccontare dopo avere bussato alla porta del professor Bigoni al DICAM.
Fig. 1 - An old steelyard and the elastica arm scale. Una vecchia bilancia stadera, basata sull’equilibrio e la bilancia elastica (foto Giuseppe Vettori, archivio Università di Trento)

Fig. 2 - The torsional gun in action: a torque is transformed into a longitudinal motion. L’arma torsionale in azione: una azione torsionale si trasforma in un moto longitudinale (foto Giuseppe Vettori, archivio Università di Trento)
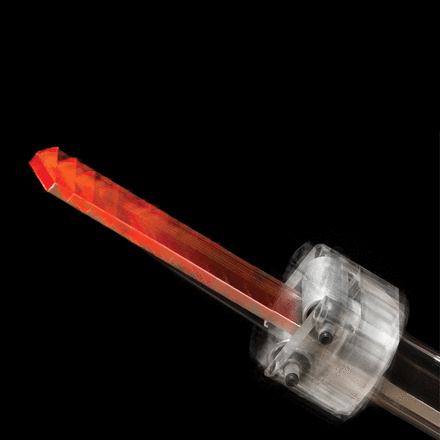
Fig. 3 - The dripping of water and of an elastic rod. La formazione di una goccia d’acqua e il dripping di una asta elastica (foto Diego Misseroni, archivio Università di Trento)