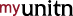Fondamenti di statistica. Per le misure e l'analisi dati in ambito industriale. Con esempi di GNU-R

Il testo fornisce le conoscenze teoriche di base di statistica e di analisi dati indispensabili per la formazione di un ingegnere industriale, affiancandole allo studio del linguaggio GNU-R e del software RStudio.
Dopo un primo capitolo introduttivo dedicato alla spiegazione del funzionamento di RStudio, nei capitoli successivi la trattazione teorica si alterna con l’analisi di casi pratici affrontati mediante GNU-R.
Gli argomenti trattati vanno dalla statistica inferenziale al concetto di qualità industriale; dalle tecniche per la regressione alla valutazione degli intervalli di confidenza; dalla progettazione degli esperimenti fattoriali allo studio dell’incertezza nelle operazioni di misura e all’analisi delle serie temporali.

Paolo Bosetti è professore presso il Dipartimento di Ingegneria industriale dell’Università di Trento

Dal Capitolo 5. La regressione (pagg. 107 -109)

5.1 Regressione lineare

Una delle operazioni più comuni nella scienza e nell’ingegneria è quella di adattare il modello analitico di un fenomeno a dei dati sperimentali. In questo contesto, “adattare” (to fit in Inglese) significa calcolare i parametri del modello che minimizzano la distanza tra il modello stesso e i dati sperimentali osservati.
In generale, in un modello analitico del tipo:

y = f (x₁, x₂, ... , x_n, c₁, c₂, ... , c_m),    (5.1)     

la variabile dipendente y è detta risposta, le variabili indipendenti x_i sono dette regressori o anche predittori, mentre le c_i sono i parametri, o anche coefficienti, del modello. Ad esempio, l’equazione y = a + bx + cx² rappresenta un modello polinomiale di secondo grado nel regressore x e con i parametri a, b, c. Efettuare la regressione di questo modello significa quindi raccogliere una serie di coppie (x, y) (entrambi variabili stocastiche) e trovare i parametri a, b, c che minimizzano la differenza tra il modello e il campione di coppie (x, y). 

5.11 Basi teoriche

Supponiamo di avere un fenomeno la cui risposta dipende da n regressori e m coefficienti, come in (5.2). Supponiamo di misurare la risposta in N combinazioni differenti dei

regressori, chiamate livelli. Per tale processo definiamo un modello statistico che correla la risposta a ciascun livello con i corrispondenti regressori: 

y_i = f(x_1i, x_2i, ... , x_{ni, C1, C2, ... , Cm) +} ε_{i =} ŷ_{1 +} ε_i, i = 1, 2, ... , N   (5.2)

dove x_ji  è il valore del j-esimo regressore alla i-esima ripetizione, ŷ₁ è il valore regredito, o regressione della risposta y_i (che è deterministico o sistematico), e ε_i è il residuo, cioè la componente puramente stocastica del modello, essendo le altre componenti deterministiche (vedi Fig. 5.1).
L’adattamento del modello (5.2) può essere effettuato minimizzando un indice di prestazione Φ definito come:

 (5.3)

Se la f () è una funzione analitica e differenziabile possiamo realizzare l’adattamento minimizzando Φ (c₁, c₂,…,c_m), cioè calcolando i coefficienti c_j che minimizzano la distanza tra la risposta misurata y_i e la risposta regredita (cioè il modello) ŷ₁.
Consideriamo il caso più semplice di una relazione lineare tra la risposta ed un unico parametro, x. Allora il modello statistico è:

y_i = (ax_i+ b) + ε_{i  (5.4)}

e i coefficienti a e b possono essere calcolati:

 (5.5)

Il minimo (che è unico!) si calcola imponendo uguali a zero le derivate parziali di  Φ:

 (5.6)

Da cui risultano i valori critici:

(5.7)

con   e ӯ le medie di x_i e y_i e con

 (5.8)

I due regressori a, b possono anche essere calcolati come soluzione della equazione matriciale Ak = y, dove A è la matrice dei regressori, k il vettore colonna dei coeffcienti e y il vettore colonna delle risposte:

 (5.9)
che può essere risolta come:

 (5.10) (5.11) (5.12)

L’ultima operazione (A^T A)_⁻¹ A^T è anche chiamata pseudo-inversa di A.
La formulazione matriciale della regressione ha il vantaggio di essere direttamente generalizzabile a qualsiasi modello polinomiale, infatti se:

 (5.13)

e i vettori colonna sono k = [c_n, c_n−1, … , c₁] ^T e y = [c₁, c₂, … , c_N] ^T , allora risulta comunque che y = A ⋅  k e quindi:

k = (A^T A)^-1A^T·  y  (5.14)

L’equazione matriciale y= A ⋅ k mostra molto chiaramente cosa si intende per modello statistico lineare: se il modello può essere rappresentato con una relazione lineare tra la matrice dei regressori e il vettore dei coefficienti, allora è un modello lineare.

Per gentile concessione di libreriauniversitaria.it edizioni